Test de numératie
Le test de numératie est une forme de test psychométrique très populaire parmi les éditeurs de tests et les processus de recrutement.
Cette épreuve cognitive évalue la capacité du candidat à analyser des problèmes mathématiques et à tirer des conclusions logiques dans un temps limité.
Il faut distinguer deux types de tests d'aptitude numérique : le test de numératie et le test de raisonnement numérique. Apprenez-en plus sur ces tests d'aptitude en consultant nos guides ou acheter notre pack complet ci-dessous.
Pack Test de Numératie
En exclusivité, nous avons créé l'unique simulation aux tests de numératie en français.
Inclus :
- Un total de 280 questions avec réponses, divisées en 6 sections.
- Questions pouvant être présentées sous forme de calculs directs ou de problèmes mathématiques.
- 50 questions d'arithmétique de base incluant les opérations de calcul de base (addition, soustraction, multiplication et division).
- 50 questions de pourcentages.
- 30 questions de fractions.
- 50 questions de conversion d'unités.
- 50 questions de puissances.
- 50 questions de séquences de nombres (suites de nombres).
- Tests pratiques à imprimer au format PDF.
- Introduction complète et guide d'étude pour chaque section, comprenant de nombreuses règles, formules et astuces mathématiques.
- Paiement sécurisé & FAQ.
Le test de numératie est le test le plus basique au sein des tests d'aptitude numérique. Il évalue les compétences des candidats à manipuler les concepts mathématiques basiques sans l'aide d'une calculatrice. De manière générale, ce test cognitif est composé des notions d'arithmétique suivantes :
| Sujets de numératie | |
|---|---|
| Pourcentages | Séquences de nombres |
| Opérations de calcul de base | Proportions et ratios |
| Fractions | Problèmes |
| Conversion d'unités | Equations |
| Puissances | Racines |
Pourcentages
Un nombre correspond à un pourcentage s'il peut être exprimé sous forme de fraction dont le dénominateur est 100 ou sous forme décimale. Par exemple, on peut exprimer un pourcentage de 30 pour cent en le notant :
- 30 %
- 0,3
Les pourcentages à connaître:
- 100 % correspond à 1 soit la totalité.
- 50 % correspond à 0,5 soit la moitié. 25 % correspond à 0,25 soit le quart.
Pour calculer le pourcentage d'une grandeur, il suffit de multiplier cette dernière par le pourcentage exprimé sous forme de fraction ou sous forme décimale. Par exemple, pour calculer 30 % d'une somme de 80 euros, on effectue
Exemple de question de pourcentage
48% des 725 élèves sont des filles. Le nombre de filles est de :
- 348
- 345
- 378
Réponse
La bonne réponse est la réponse A.
Prendre 48% cela revient à multiplier par 0,48, donc :
0,48 x 725 = 348 ou
Opérations de calcul de base
L'addition
Pour additionner deux nombres, on additionne successivement les chiffres des unités, les chiffres des dizaines en tenant compte d'une possible retenue et les chiffres des centaines en tenant également compte de la possibilité d'une retenue issue des chiffres des dizaines.
Exemple

Pour additionner des nombres décimaux, on additionne d'abord la partie décimale (à droite de la virgule), puis la partie entière (à gauche de la virgule).
Exemple
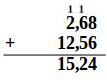
La soustraction
Exemple

La multiplication
Pour multiplier un nombre par 10, 100, 1 000, etc., on ajoute au nombre autant de zéros que le nombre multiplicateur a, ou on décale la virgule vers la droite d'autant de chiffres qu'il y a de zéros au multiplicateur.
Exemples
25 x 10 = 250
75 x 1000 = 75000
12,25 x 10 = 122,5
Pour multiplier un nombre par 5, 50, etc., on divise le nombre par 2 et on multiplie le résultat par 10, 100, etc.
64 x 5 = (64 / 2) x 10 = 32 x 10 = 320
Par conséquent : pour diviser un nombre par 5, 50, etc., on divise le nombre par 10, 100, etc., et on multiplie le résultat par 2.
64 / 5 = (64 / 10) x 2 = 6,4 x 2 = 12,8
Pour multiplier un nombre par 0,05 ; 0,005, etc., on divise le nombre par 2 puis on divise le résultat par 10, 100, etc.
64 x 0,05 = (64 / 2) / 10 = 32 / 10 = 3,2
Par conséquent : pour diviser un nombre par 0,05 ; 0,005, etc., on multiplie le nombre par 2, puis on multiplie le résultat par 10, 100, etc.
64 / 0,05 = (64 x 2) x 10 = 128 x 10 = 1280
Pour multiplier un nombre par 25, on le divise par 4 et on multiplie le résultat par 100.
32 x 25 = (32 / 4) x 100 = 800
Pour multiplier un nombre par 2,5 ; on le divise par 4 et on multiplie le résultat par 10.
32 x 2,5 = (32 / 4) x 10 = 80
Par conséquent : pour diviser un nombre par 25, on le multiplie par 4 puis on divise le résultat par 100.
32 / 25 = (32 x 4) / 100 = 1,28
Pour multiplier un nombre par 101, 1001, etc., on multiplie le nombre par 100, 1 000, etc., et on ajoute le nombre au résultat.
25 x 101= 2500 + 25 = 2525
Pour multiplier un nombre par 9,99, etc., on multiplie le nombre par 10, 100, etc., et on retranche le nombre du résultat.:
25 x 99 = 2500 - 25 = 2475
Pour multiplier un nombre par 0,20 on divise le nombre par 5; c'est-à-dire que selon la règle de multiplication d'un nombre par 5, on divise le nombre par 10 et on multiplie le résultat par 2.
25 x 0,20 = 2,5 x 2 = 5
La division
| Critères de divisibilité | |
|---|---|
| Règles | Exemples |
| Un nombre est divisible par 5 si le chiffre des unités est 0 ou 5. | 750/5 = 150 |
| Un nombre est divisible par 3 si la somme des chiffres est divisible par 3. | 534 → 5 + 3 + 4 = 12 |
| Un nombre est divisible par 4 si le nombre formé par les 2 derniers chiffres est divisible par 4. | 1612, 54760,... |
| Un nombre est divisible par 6 s'il est divisible par 2 et 3. | 72/6 = 12 72/2 = 36 72/3 = 24 |
| Un nombre est divisible par 9 si la somme des chiffres est divisible par 9. | 84321 → 8 + 4 + 3 + 2 + 1=18 |
| Un nombre est divisible par 10 si le chiffre des unités est un zéro. | 532985920 |
| Un nombre est divisible par 11 si la somme de ses chiffres de rang pair soustraite de la somme de ses chiffres de rang impair est nulle ou un multiple de 11. Donc 13754 est divisible par 11. | 13574 : + 7 = 10 (1 + 5 + 4) = 10 - 10 = 0 |
| Un nombre est divisible par 20 s'il se termine par 00-20-40-60-80. | 380, 40348260,... |
| Un nombre est divisible par 25 s'il se termine par 00-25-50-75. | 525, 89504350,... |
Priorité des opérations
Conventions qui établissent l'ordre selon lequel on doit opérer lorsqu'on cherche la valeur d'une chaîne d'opérations.
L'ordre à suivre est le suivant :
- Effectuer les opérations entre parenthèses (P)
- Effectuer les exponentiations (E)
- Effectuer les multiplications et les divisions (MD)
- Effectuer les additions et les soustractions (AS)
Un moyen mnémotechnique pour retenir cet ordre est l'acronyme PEMDAS.
Exemple
28 – 3 (12 ÷ 4) – 4²
= 28 – 3 × 3 – 4²
= 28 – 3 × 3 – 16
= 28 – 9 – 16
= 28 – 25
= 3
Fractions
Composantes d'une fraction
La fraction est composée d'un numérateur (a) et d'un dénominateur (b).
Fractions équivalentes
Il est important de se rappeler qu'il existe plusieurs façons de représenter la même fraction. Par exemple, les fractions 1/2 et 2/4 sont tout à fait équivalentes. Comment passe‐t‐on d'une fraction à l'autre tout en conservant la relation d'équivalence ?
Une fraction reste équivalente si le numérateur et le dénominateur sont multipliés ou divisés par le même nombre.
Exemple
Simplification de fractions
Une fraction est écrite sous forme simplifiée si le numérateur et le dénominateur n'ont aucun facteur commun. En d'autres mots, sous forme simplifiée, il est impossible de trouver un nombre qui soit diviseur à la fois du numérateur et du dénominateur.
Exemple
La fraction n'est pas écrite sous forme simplifiée puisqu'il existe des nombres qui divisent 120 et 200. Le plus grand diviseur (facteur) commun de 120 et de 200 est 40, d'où
Puisque le numérateur et le dénominateur sont divisés par le même nombre (40), la fraction est équivalente à
. De plus
est la forme simplifiée de
puisque aucun facteur commun n'existe pour 3 et 5.
Une simplification peut s'effectuer en plusieurs étapes si on ne reconnaît pas, à prime abord, le plus grand facteur commun du numérateur et du dénominateur.
Exemple
Règles de fractions
| Sujet | Règle | Exemple |
| Règle d'addition et de soustraction de fractions |  | |
| La règle d'addition et de soustraction des fractions n'est applicable que si les deux fractions possèdent le même dénominateur, ce qui ne sera généralement pas le cas. Il faut alors réécrire les fractions en fractions équivalentes ayant un dénominateur commun. |
Ces fractions ne peuvent être additionnées avant de les avoir réécrites avec un dénominateur commun. Le plus petit commun multiple des nombres 3 et 5 est 15. 15 sera donc le commun dénominateur | |
| Règle de multiplication de deux fractions | Contrairement à l'addition de fractions, les dénominateurs n'ont pas besoin d'être communs afin de les multiplier. | |
| Règle de division de deux fractions | La règle permet de transformer une division en multiplication |  |
Bon à savoir
Le fait de travailler avec des fractions ne modifie en rien la priorité des opérations.
Exemple
Un nombre entier peut toujours être écrit sous forme de fraction si une opération doit être effectuée entre celui‐ci et une fraction.
Exemple
Évitez de travailler avec des nombres mixtes… transformez‐les plutôt en fractions simples.
Exemple
Conversion d'unités
Voici ci-dessous plusieurs tableaux représentant les unités différentes (longueur, masse, temps, etc.).
Conversions par puissance de dix (multiples d'une unité) :
| Préfixe | Tera | Giga | Mega | Kilo | hecto | centi | milli | nano | pico |
| Facteur | 1012 | 109 | 106 | 103 | 102 | 10-2 | 10-3 | 10-9 | 10-12 |
Unités de longueurs
| gigamètre | gm | 109 m | 1000 000 000 m |
| mégamètre | Mm | 106 m | 1000 000 m |
| kilomètre | km | 103 m | 1000 m |
| hectomètre | hm | 102 m | 100 m |
| décamètre | dam | 10 m | 10 m |
| mètre | m | 1 m | 1m |
| décimètre | dm | 10-1 m | 0,10 m |
| centimètre | cm | 10-2 m | 0,100 m |
| millimètre | mm | 10-3 m | 0,1000 m |
| micromètre | µm | 10-6 m | 0,1000 000 m |
| nanomètre | nm | 10-9 m | 0,1000 000 000 m |
Unités de masse
| 1 tonne | t | 106 g | 1000 000 g |
| 1 kilogramme | kg | 103 g | 1000 g |
| 1 gramme | g | 1 g | 1 g |
| 1 milligramme | mg | 10-3 g | 0,001 g |
| 1 microgramme | µg | 10-6 g | 0,000 001 g |
| 1 nanogramme | ng | 10-9 g | 0,000 000 001 g |
Unités de mesure du temps
| 1 millénaire | 1000 années |
| 1 siècle | 100 années |
| 1 décennie | 10 années |
| 1 lustre | 5 années |
| 1 année | 365 jours |
| 1 semaine | 7 jours |
| 1 jour | 24 heures |
| 1 heure | 60 minutes ou 3600 secondes |
| 1 minute | 60 secondes |
Unités d'aire
| km² | hm² | dam² | m² | dm² | cm² | mm² |
| 1000 000 | 10 000 | 100 | 1 | 0,01 | 0,0001 | 0,000001 |
Conversion d'unités de surface et de volume
| 1 mm | 10-3 m |
| 1 mm² | 10-6 m |
| 1 mm³ | 10-9 m |
Puissances
Lois des puissances
Rappel :
a0 = 1
a1 = a
a - 1 = 1/a
an = a × a × ... × a (n facteurs)
a - n = 1 / an
| Formule | Exemple |
| am × an = am+n | |
Conseil
Afin de gagner du temps pendant une épreuve de numératie, AptitudeTests vous conseille d'apprendre ce tableau par coeur :
| 0² = 0 | 5² = 25 | 8² = 64 | 11² = 121 | 14² = 196 |
| 1² = 1 | 6² = 36 | 9² = 81 | 12² = 144 | 15² = 225 |
| 4² = 16 | 7² = 49 | 10² = 100 | 13² = 169 | 16² = 256 |
Séquences de nombres
Les questions de séquences de nombres sont fréquemment utilisées dans les tests de numératie. Elles permettent d'évaluer les capacités du candidat à comprendre la logique numérique ainsi qu'à évaluer son potentiel en calcul mental. Les suites de nombres peuvent combiner plusieurs opérations de calculs de base (addition, soustraction,...), ou répondre à une logique utilisant les propriétés des chiffres (pair, impair, premier,...).
Ci-suivent, des exemples de série pouvant apparaître dans des tests de numératie :
| Suites générales | Suite de nombres pairs | 2, 4, 6, 8, 10,12,... |
| Suite de nombres impairs | 1, 3, 5, 7, 9,11,13,... | |
| Nombres premiers | 2, 3, 5, 7, 11 ,13,17,... | |
| Multiples de 3 (ou tout autre chiffre) | 3, 6, 9, 12, 15,18,... | |
| Suites arithmétiques suite de nombres où on passe d'un terme au suivant en ajoutant toujours le même nombre | Suite de raison 3 (c-à-d +3) | 2, 5, 8, 11, 14, 17,... |
| Suite de raison -3 (c-à-d -3) | 17, 14, 11, 8, 5, 2,... | |
| Suites géométriques suite de nombres où on passe d'un terme au suivant en multipliant toujours par le même nombre | Suite de raison 4 (c-à-d +4) | 2, 8, 32, 128, 512,... |
| Suite de raison -4 (c-à-d -4) | 512, 128, 32, 8, 2,... | |
| Suites avec opérations entre les nombres | Addition du nombre précédent | 1, 2, 3, 5, 8, 13, 21,... |
| Suites l'une dans l'autre | Deux suites en une | 2, 3, 4, 6, 6, 9, 8, 12,10,... |
| Suites plusieurs opérations | Suites à deux opérations (+3, x2) | 1, 4, 8, 11, 22, 25, 50,... |
| Suites à trois opérations (+2, x3, -1) | 1, 3, 6, 5, 7, 21, 20,... |
Proportions et Ratios
Proportions
Proportionnalité : En mathématiques, on dit que deux séries de nombres sont proportionnelles quand on peut passer de l'une à l'autre en multipliant ou en divisant la première par une même constante non nulle.
Règle de trois ou règle de proportionnalité : Cette règle permet de calculer un produit à partir de 3 nombres donnés en suivant la formule suivante :
Exemple simple
| Poids de tomates (kg) | 1 | 2 | 3 | 4 | 5 |
| Prix | 2 | 4 | 6 | 8 | 10 |
Le coefficient de proportionnalité est de 2.
Exemple de question de test
| Transporteur de Kuehne + Nagel | |||
| Camions | Consommation Nombre de litres pour 100 km | Nombre de km par jour | |
| Remorque 20'' | Remorque 40'' | ||
| Camion A | 20 | 30 | 150 |
| Camion B | 17 | 21 | 120 |
| Camion C | 18 | 23 | 135 |
Combien de litres de carburant le camion B consomme-t-il de plus avec la remorque de 40'' par rapport à la remorque de 20" ?
- 4,5
- 3,9
- 4,8
- 5,1
Réponse
La bonne réponse est la réponse C.
En premier lieu, il est nécessaire de créer une équation en utilisant la règle de trois afin de déterminer le nombre de litres que consomme le camion B avec la remorque de 20'' en une journée :
Le camion B consomme donc 20,4 litres de carburant par jour avec la remorque de 20''.
Ensuite il faut effectuer le même calcul pour la remorque de 40'' :
Le camion B consomme donc 25,2 litres de carburant par jour avec la remorque de 40''.
→25,2 litres - 20,4 litres = 4,8 litres
Ratios
Un ratio est une relation quantitative entre deux nombres qui décrit combien de fois une valeur peut en contenir une autre. Les ratios sont utilisés intuitivement dans la vie quotidienne, notamment dans les recettes de cuisine, ou encore pour calculer la taille des écrans d'ordinateurs et de smartphones.
Conversion des nombres décimaux les plus connus en ratios :
- 0,1 = 1;10 ou 1 pour 10
- 0.2 = 1;5 ou 1 pour 5
- 0.25 = 1;4 ou 1 pour 4
- 0.33 = 1;3 ou 1 pour 3
- 0.5 = 1;2 ou 1 pour 2$
Exemple d'exercice simple de ratio apparaissant dans les tests de numératie
Dans un moteur, un ratio huile-essence de 3;100 est nécessaire. Si 200 ml d'essence sont versés dans le moteur, combien d'huile faut-il ajouter ?
- 8 ml
- 5 ml
- 6 ml
- 15 ml
Réponse
La bonne réponse est la réponse C.
Dans ce type de questions, la réponse peut se trouver de manière intuitive, car il suffit de doubler les valeurs de manière à trouver la bonne réponse. Dans des exercices plus compliqués, il est nécessaire d'effectuer un calcul simple qui permettra de trouver la valeur demandée.
Exemple plus complexe
Quel est le ratio du taux de mortalité entre les années 1950 et 1990 ?
| Année | Taux brut de natalité (%) | Taux brut de mortalité (%) | Taux d'accroissement naturel (%) |
| 1950 | 20 | 24 | 5 |
| 1960 | 29 | 23 | 6 |
| 1970 | 31 | 21 | 10 |
| 1980 | 38 | 19 | 19 |
| 1990 | 47 | 18 | 29 |
- 2;3
- 4;3
- 5;6
- 2;4
Réponse
La bonne réponse est la réponse B.
Ici, il est nécessaire de calculer afin de trouver la bonne réponse. En premier lieu, il faut diviser les deux valeurs des taux de mortalité demandés, c'est-à-dire 24/18, ce qui est égal à 1,3333. Afin de transformer cette fraction en ratio (l'idéal serait de retenir cette conversation par coeur, celle-ci étant souvent utilisée), Il faut multiplier la fraction par un certain nombre, de manière à obtenir un nombre entier. Donc pour cette exemple : 1,3333 x 3 = 4, le ratio équivaut donc à 4;3, réponse B.
Problèmes
Un problème mathématique ou quantitatif se définit comme étant une question pouvant être résolue à l'aide des éléments donnés dans l'énoncé. Il est généralement constitué d'un ensemble d'informations présentées sous diverses formes (texte, tableau, dessin,...), faisant l'objet d'un questionnement, qui, afin d'être résolu, nécessite l'implication de notions et/ou d'outils mathématiques. Dans un test de numératie, le problème présenté peut généralement se résoudre de manière intuitive ou avec des notions mathématiques de base telles que présentées plus haut.
Exemple
Deux camions ont été conduits sur un parcours de 1 680 kilomètres (km). Le premier camion a parcouru en moyenne 14 km au litre de carburant pendant le voyage et le second camion a parcouru en moyenne 12 km au litre. Combien de litres d'essence, le second camion a-t-il consommé de plus que le premier ?
- 10
- 20
- 30
- 40
- Ce n'est pas possible de le dire avec les informations fournies.
Réponse
La bonne réponse est la réponse B.
Afin de résoudre le problème, il est nécessaire de calculer le nombre de litres utilisés au total pour chaque camion, et ensuite de calculer la différence entre eux.
Camion A : 1680/14 = 120
Camion B 1680/12 = 140
140 - 120 = 20, réponse B.
Exemple 2
Un livre est disponible à la librairie locale en version digitale (eBook) pour 5,90 Euros, et en version broché pour 13,40 Euros. Le livre peut aussi être obtenu par Amazon avec une réduction de 15 %, plus 2,50 Euros pour les frais d'envoi. Quelle est la différence de prix entre la version digitale et la version brochée commandée sur Amazon ?
- 8,14 Euros
- 9,83 Euros
- 6,99 Euros
- 7,45 Euros
- 7,99 Euros
Réponse
La bonne réponse est la réponse E.
Afin de calculer la différence entre les deux formats, il faut d'abord calculer le prix du livre avec la réduction et les frais d'envois.
13,40 x 15/100 = 2,01
13,40 - 2,01 + 2,50 = 13,89
13,89 - 5,90 = 7,99
Equations
Qu'est-ce qu'une équation?
Une équation est composée d'une ou plusieurs inconnues (nombre dont on ne connaît pas la valeur), et d'informations sur ces inconnues permettant de calculer leur valeur.
Exemple d'équation simple :
3x = x + 72
3x - x = 72
x (3 - 1) = 72
2x = 72
x = 72/2
x = 36
Il est possible de simplifier la compréhension de la lecture d'une équation en le transformant en question verbale. Ainsi, l'équation proposée ci-dessus se lit : Je suis un nombre inconnu. Je suis égal au tiers de mon nombre plus 24. Qui suis-je ?
Identités remarquables : trois formules de base (il en existe plus), appelées identités remarquables, sont à connaître car elles permettent de faciliter grandement certains calculs.
La 1re est : (a + b)² = a² + 2ab + b²
La 2e est : (a – b)² = a² - 2ab + b²
La 3e est : a² – b² = (a + b)(a - b)
Ces formules peuvent être appliquées dans les deux sens.
Exemple : (2 + 3)² = 4 + 12 + 9 = 25
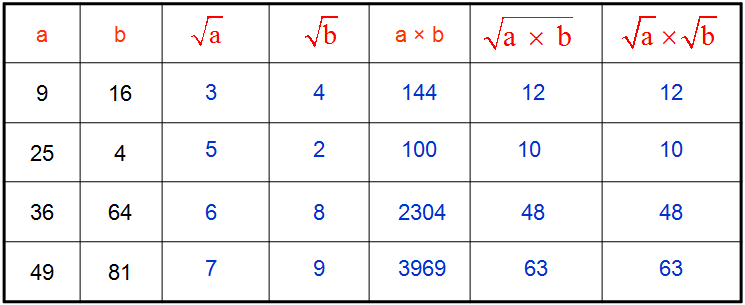
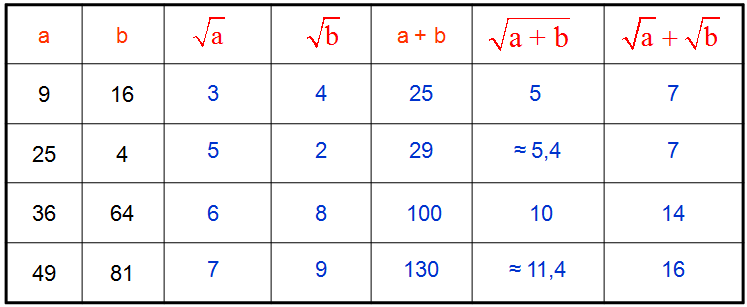
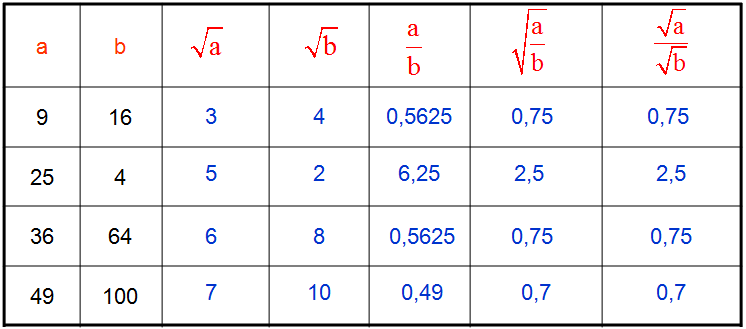
Racines
Voici quelques tableaux récapitulatifs concernant les racines :
Pour quels emplois le test de numératie est-il utilisé ?
Le test de numératie est utilisé pour des postes et formation non managérials exigeant des capacités de calcul mental efficaces dans n'importe quelle situation, notamment dans des emplois où le candidat est appelé à utiliser ses connaissances quotidiennement et sous pression. Métiers requérant ces compétences :
- Métiers liés à la vente
- Chauffeurs de bus et de trains
- Assistants techniques (help desk support)
- Services à la clientèle
- Infirmiers, sages-femmes et ambulanciers paramédicaux
- Soldats et autre personnel militaire
- Steward et hôtesse de l'air
- Surveillant pénitentiaire
Les principaux éditeurs de tests de numératie
| Editeurs | Tests |
|---|---|
| SHL | SHL Verify Checking & Calculation Tests |
| Math Problem Solving | |
| cut-e | scales eql - Numeracy |
| Criteria | Criteria Basic Skills Test (CBST) |
| Wonderlic | Wonderlic Basic Skills Test (WBST) |
| Thomas International | Test d'Intelligence globale (TIG) |
| Saville Consulting | Administrative Numerical Comprehension |
| Saville Consulting | Customer Numerical Comprehension |
| Saville Consulting | Commercial Numerical Comprehension |
| Saville Consulting | Operational Numerical Comprehension |
| Criterion | B2C Numerical Ability Test |
| Criterion | CWS Numerical Ability Test |
| Selective Hiring | Basic Math Skills |
| HRdirect | SkillSeries Math Test |
| TAFE SA | TABE Numeracy Test |













